ecsimsw
HashTable 원리와 구현 본문
Hashing / HashTable
key 값을 조작해서, 배열의 인덱스와 매핑한다면, key에 해당하는 value 값을 배열의 인덱스에 접근하는 것처럼, O(1)의 비용으로 가져올 수 있을 것이다.
예를들어, 과일 과게에서 과일의 바코드 Id와 과일 명을 담는 테이블을 만든다고 치자.
102 -> apple
543 -> banana
87426 -> orange
9 -> grape
왼쪽이 id, 오른쪽이 상품명이라고 하면, 과일 과게 주인은 다음과 같은 표를 만들 수 있다.

만약 가게 주인이 id에 해당하는 과일 이름을 알고 싶다면, id를 순차적으로 하나씩 확인하고, 해당 id의 과일 이름을 가져와야 하는 것이다.
혹은 이런 표를 만들면 어떨까.

id의 끝자리를 인덱스로 해서 아래처럼 표를 그리면 가게 주인은 더이상 표를 쭉 탐색하지 않아도, 규칙에 따라 끝자리에 해당하는 인덱스 칸만 탐색하는 것으로 과일의 이름을 알 수 있는 것이다.
index = key % 10
fruit_name = table[index]
이렇게 key와 인덱스를 매핑하는 방법을 해싱이라고 한다.

Collision
위의 예시를 이어서, 이번에는 가게에 id가 4529인 멜론이 들어왔다고 가정해보자.
표의 인덱스 9는 이미 포도가 들어가있어, 가게 주인의 꼼수에 문제가 생겼다. 이렇게 동일한 입력 값이 같은 key 값을 가져 저장하지 못하는 상황을 충돌이라고 한다.
이 충돌을 해결하기 위한 방법으로 크게 Separate Chaining 방식과, Open Addressing 방식이 있다.
Separate Chaining
충돌 시 해시 테이블 인덱스에 연결 리스트를 이용해서 여러 값을 연결한 형태로 저장한다. 상대적으로 적은 메모리를 사용하나, 해시 함수가 고른 분포를 만들지 못하면 성능에 치명적이다.
이를 테면, 모든 과일의 hash 값이 한 인덱스에 몰려 모든 value가 연결된다면, value를 찾아내는데는 연결 리스트를 모두 탐색해야하므로 최악의 경우 O(n)의 성능을 갖을 수 있다.

Open addressing
충돌 시, 연결이 아닌 비어있는 인덱스를 찾아 데이터를 저장하는 방식이다.
비어있는 인덱스 중 데이터가 저장될 공간을 찾는 규칙은 다음 세가지 방식으로 할 수 있다.
| 선형 탐색(Linear Probing) : 비어있는 인덱스 n개를 후의 비어있는 슬롯에 노드를 저장한다. ( -> h(k), h(k)+n, h(k)+2n, h(k)+3n 제곱 탐색(Quadratic Probing): 충돌이 일어난 인덱스의 제곱을 한 해시에 데이터를 저장한다. -> h(k), h(k)+1^2, h(k)+2^2, h(k)+3^2 이중 해시(Double Hashing): 다른 해시 함수를 한 번 더 적용한 해시에 데이터를 저장한다. -> h(k,i) = (h(k) +i*h'(k)) % m |
Linear Probing
선형 탐색에서 n=1, 즉 충돌 시 다음 비어있는 공간에 데이터를 넣는 방식으로 위 예시 충돌 상황을 처리해보자.
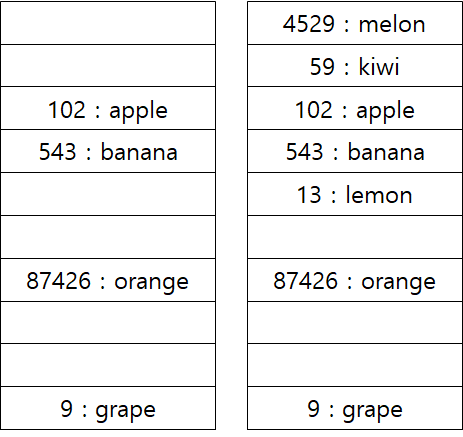
위 그림에서 왼쪽은 원본 예시 상황이고, 여기에 4529 / 13 / 59를 추가하면 오른쪽 그림처럼 데이터가 저장된다.
4529는 인덱스 9에서 충돌이 일어나 다음 비어있는 칸, index 0에 저장되고, 13 역시 543의 바로 다음 칸 index 4, 59는 index 9, index 0 모두 값이 존재하므로 그 다음 칸인 index 1 에 저장된 것이다.
선형 탐색에서의 Search
선형 탐색에서의 탐색은 원래 해시 값에 해당하는 인덱스를 탐색하고, key가 일치하지 않으면 규칙에 맞춰 다음 칸, 또 다음 칸을 순서대로 탐색하는 것이다.
만약 탐색하는 칸이 비어있다면, 해당 key는 아직 저장이 안된 것을 알 수 있다.
이를 수도 코드로 나타내면 다음과 같다.
while(Node != null){ // 탐색 노드가 비어있다면 searchKey가 아직 저장이 안된 것임
if(Node.key == searchKey) return Node.value;
Node = Node.next; // 규칙에 맞는 다음 노드
}

선형 탐색의 단점이 여기에 있다.
1. Primary clustering
비어있지 않은 슬롯이 연속하게 되면 탐색에도 오래걸릴 뿐 아니라, 규칙에 따라 다음 빈 곳을 찾는 추가에도 많은 시간이 걸린다. 또 한번 군집이 시작되면 점점 더 커진다.

2. 삭제 처리
선형 탐색은 데이터 추가 시 규칙에 따라 슬롯을 탐색하고, 처음 만나는 빈 슬롯에 데이터를 저장한다. 그렇기 때문에 탐색 시에도 비어있는 슬롯을 만나면 데이터가 저장되지 않았다고 생각하고 탐색을 종료한다.
그런데 만약 중간 데이터가 삭제된 상황이라면 어떻게 할 것인가.

선형 탐색으로 해시 테이블을 만든다면 이를 해결하기 위해 삭제된 노드에 Dummy node를 포함시켜 탐색 시 다음 index를 연결하는 역할을 하도록한다.
이 Dummy node도 너무 많아질 경우 쓸데없는 탐색 시간과 공간이 낭비되므로, hash를 리빌딩하여 Dummy node를 삭제하는 과정이 필요하다.
자바에서의 Hash
자바8의 HashMap은 충돌을 어떤 방식으로 처리할까.
1. Seperate Chaining
자바7까지 HashMap에 Separate Chaining을 사용한 것은 같지만, 자바8부터는 버킷 당 8개 이상의 데이터가 쌓이면 링크드 리스트에서 트리로 변경한다. (이때 트리 탐색 대소 판단 기준은 해시 함수 값이다.)
그리고 데이터가 삭제되어 6개에 이르면 트리에서 다시 링크드 리스트로 변경한다.
이는 노드가 많을 경우 탐색 성능을 위해서는 트리가 우수하지만, 노드가 적을 경우에 트리는 리스트보다 메모리 사용량이 많고, 탐색 성능에서도 크게 차이가 없기 때문이다.
또, 리스트->트리, 트리->리스트를 8/6으로 차이를 둔 것은 만약 차이가 1이라면 한 쌍이 추가, 삭제가 반복될 경우 자료 구조를 매번 변경해야하는 오버헤드를 낳을 수 있어 2개의 차이를 뒀다고 한다.
2. 해시 버킷 동적 확장
해시 버킷의 개수가 적으면 메모리를 아낄 수 있고, 버킷이 많으면 해시 충돌을 줄여 성능을 높일 수 있을 것이다.
자바의 HashMap에서는 데이터의 개수가 일정 개수 이상이 되면 버킷의 개수를 2배로 늘려 성능 손실 문제를 해결한다고 한다. 이때 어느정도 예측 가능한 상황의 경우 버킷의 최초 개수와 임계점을 직접 지정할 수 있다. (디폴트는 16개, 75%이다)
최초 버킷의 수는 말그대로 최초 Entry 개수를 말하고, 임계점(load Factor)는 현재 Entry 개수의 몇 배수가 되면 버킷 확장을 실행할까를 결정한다.
예를 들어, 버킷이 100개이고, load factor가 0.87이면, 데이터의 개수가 87개 이상일 때, 버킷의 개수를 200으로 확장하는 것이다.
구현
자바로 간단하게 Seperate Chaining을 구현해봤다.
class HashTable {
class Node {
String key;
String value;
public Node(String key, String value) {
this.key = key;
this.value = value;
}
}
private LinkedList<Node>[] table;
public HashTable(int size) {
table = new LinkedList[size];
}
Long getHashCode(String key) {
Long hashCode = 0L;
for (char c : key.toCharArray()) { hashCode += (long) c; }
return hashCode;
}
public int getIndex(Long hashCode) {
return (int) (hashCode % table.length);
}
Node searchNode(int index, String key) {
LinkedList<Node> indexedList = table[index];
for (Node n : indexedList) {
if (n.key == key) { return n; }
}
return null;
}
public void put(String key, String value) {
Long hashCode = getHashCode(key);
int index = getIndex(hashCode);
if (table[index] == null) {
table[index] = new LinkedList<Node>();
table[index].add(new Node(key, value));
}
else {
Node searched = searchNode(index, key);
if (searched != null) { searched.value = value; }
else { table[index].add(new Node(key, value)); }
}
}
public String get(String key) {
Long hashCode = getHashCode(key);
int index = getIndex(hashCode);
Node searched = searchNode(index, key);
if (searched == null) { return ""; }
else { return searched.value; }
}
}
참고
Hashtable의 이해와 구현 #1
해쉬 테이블의 이해와 구현 (Hashtable) 조대협 (http://bcho.tistory.com) 기본적인 해쉬 테이블에 대한 이해 해쉬 테이블은 Key에 Value를 저장하는 데이타 구조로, value := get(key)에 대한 기능이 매우매우..
bcho.tistory.com
Hash, Hashing, Hash Table(해시, 해싱 해시테이블) 자료구조의 이해
0_HJVxQPQ-eW0Exx7M.jpeg DATA들이 사용하기 쉽게 정리되어 있다. 자료구조는 도대체 무엇일까? 자료구조(Data-Structure)는 데이터들의 모임, 관계, 함수, 명령 등의 집합을 의미한다. 더 쉽게 표현하자면, 1)
velog.io
'Language > Java, Kotlin' 카테고리의 다른 글
| 자바의 동기화 방식 (1) | 2020.12.24 |
|---|---|
| 자바 불변 객체와 메모리 구성 (6) | 2020.11.22 |
| 자바 바이트 코드 분석하기 (0) | 2020.07.06 |
| 자바는 문자열의 끝을 표시하지 않는다. (1) | 2020.04.13 |
| Getter랑 Setter를 왜 써야할까? (15) | 2020.04.02 |

